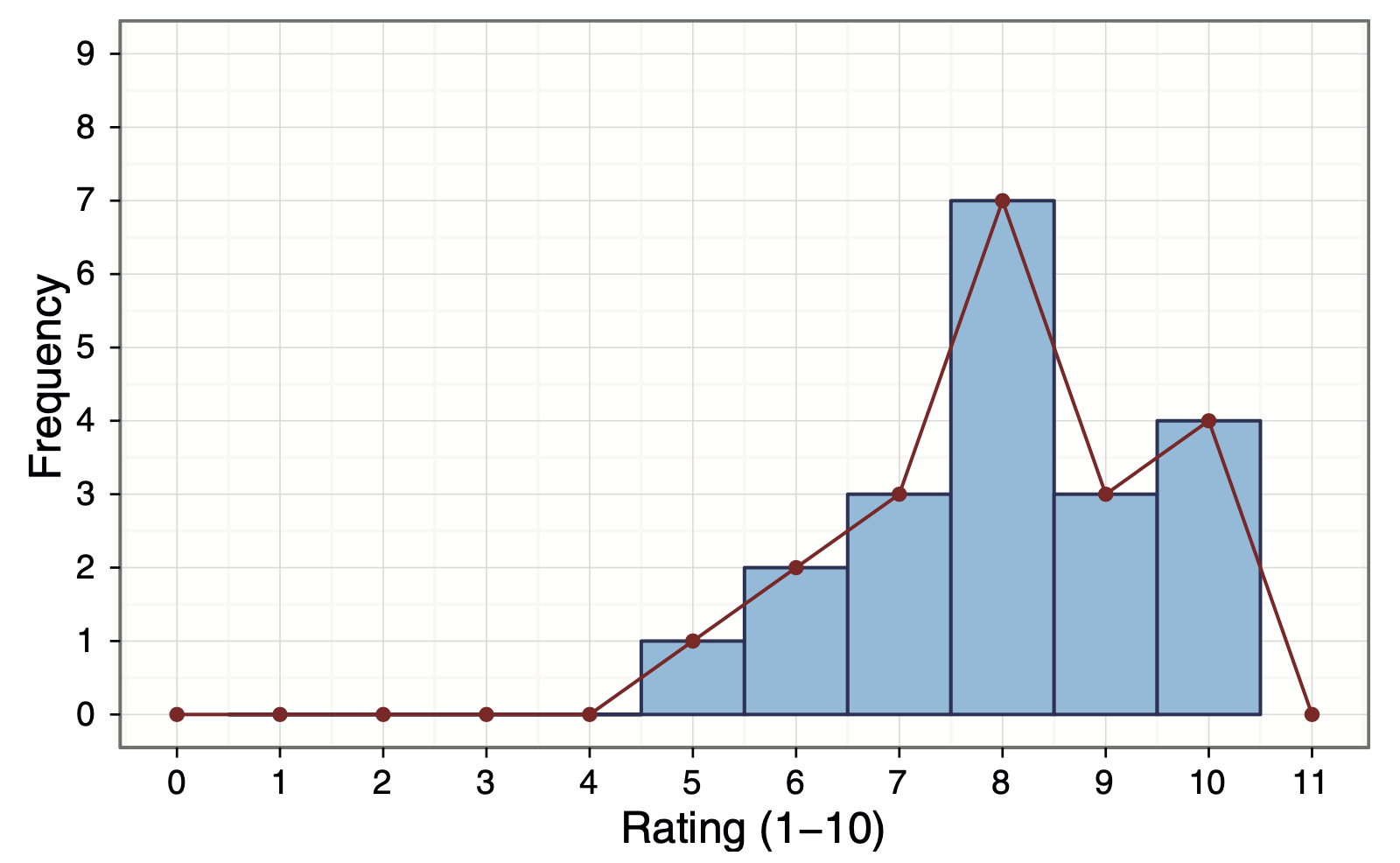
Throwing Shapes

2nd SARA Statistics Winter School, 23-27 Jan 2026

Idealised Distributions

The beauty of data is that we can use samples to estimate the shape of the distribution of scores in the entire population.

Relative Frequencies

It is reasonable to assume that the relative frequencies in the sample will be similar to those in the population.
We do not need to know the actual frequencies in the population, we work instead with relative frequencies.

Probability Distribution

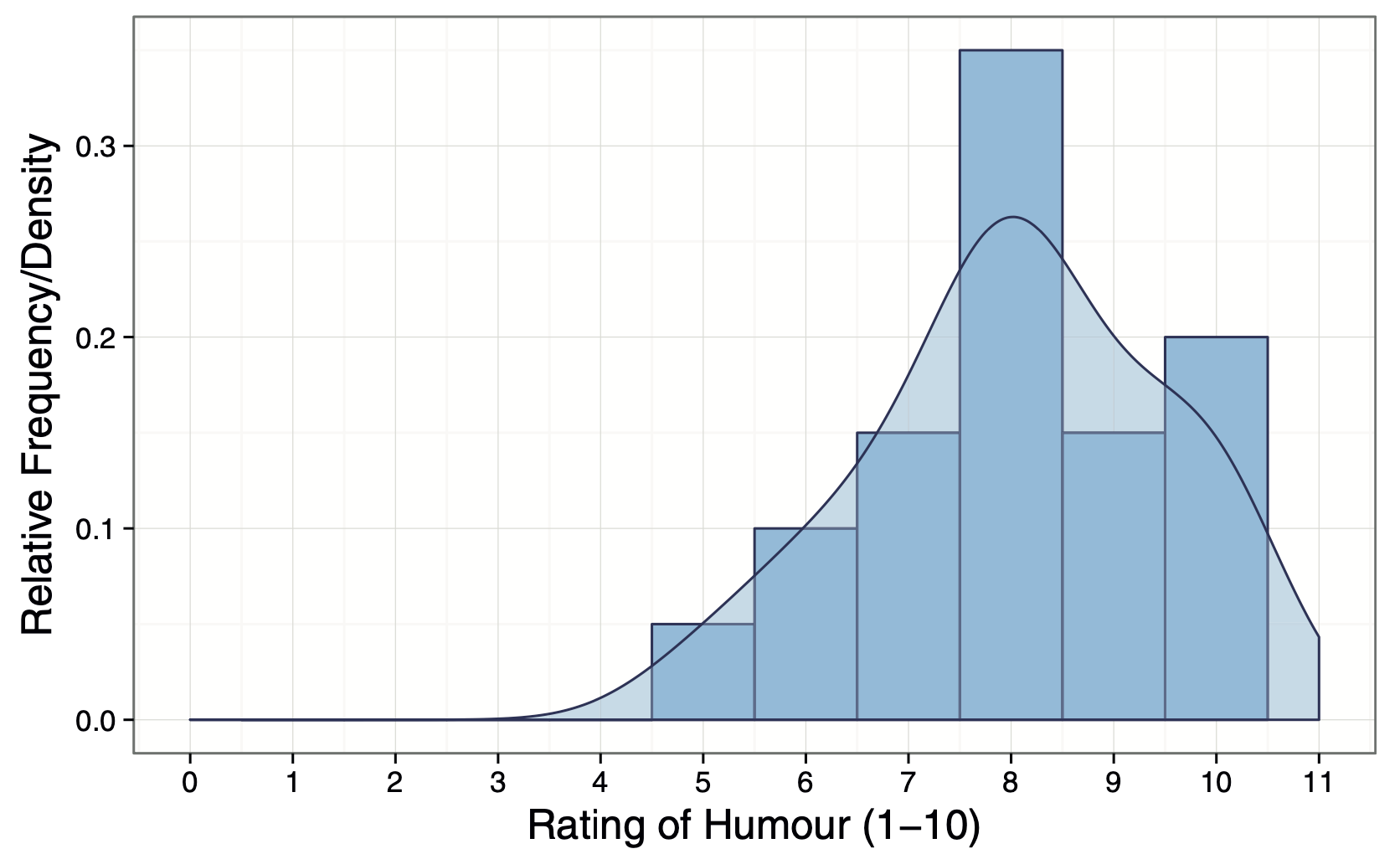
Common Distributions

Common shapes of distributions are
- normal distribution,
- \(t\)-distribution,
- \(chi-square\) (\(\chi^2\)) distribution,
- \(F\)-distribution.
Each have a specific shape that can be described by an equation.

Symmetrical/Normal Distribution

The curve is symmetrical if we draw a vertical line through the centre of the distribution then it looks the same on both sides.

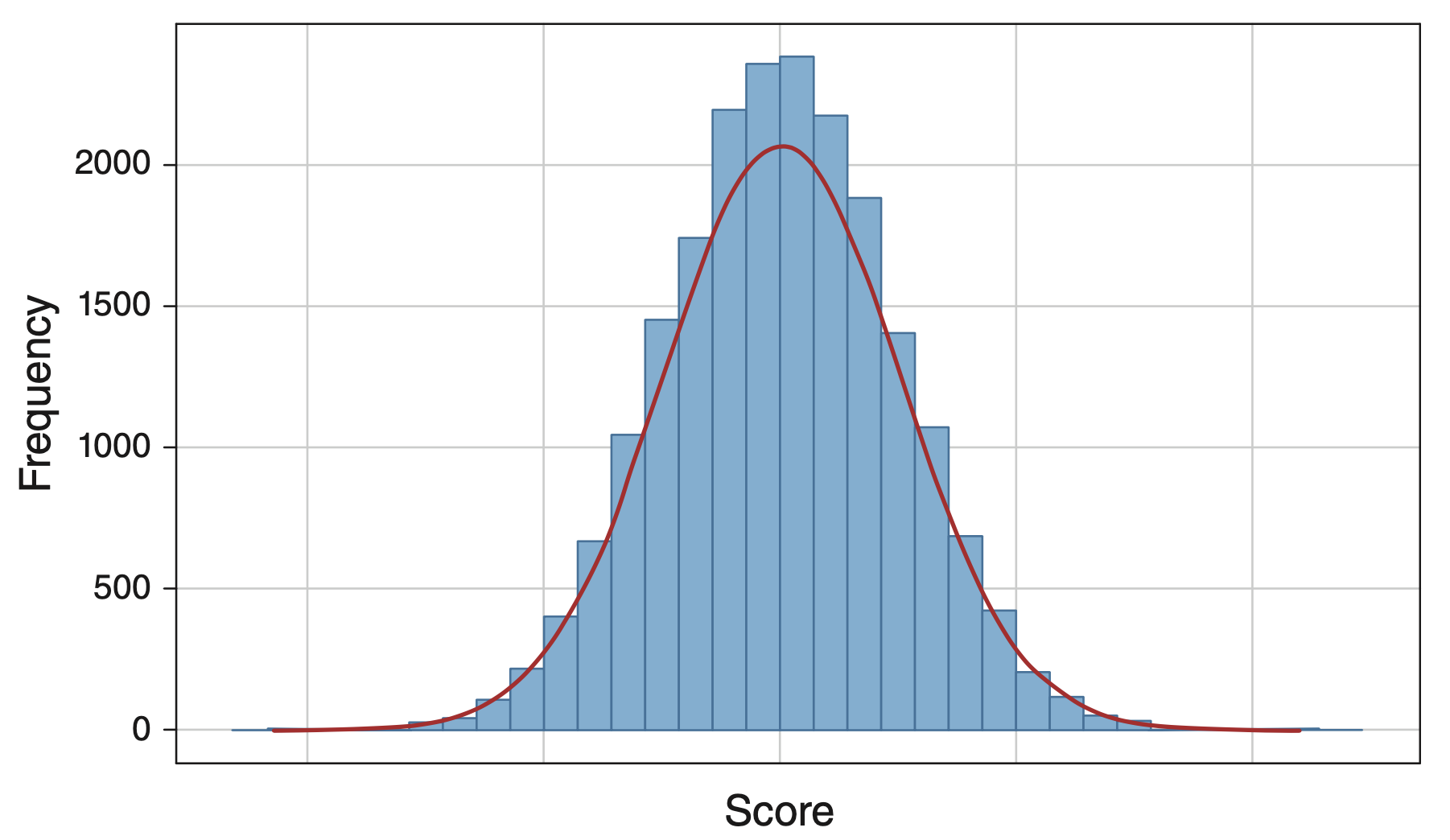
Shape of the Distribution

Central Tendency: Mean determines the center of the distribution
Variability: Standard deviation width or spread of the distribution.
68-95-99.7 Rule:
- 68% of data falls within ±1σ of the mean.
- 95% within ±2σ.
- 99.7% within ±3σ.

Practice

Plot the Normal Distribution
Central Tendency and Variability
Visualizing Central Tendency
Interpret the Results

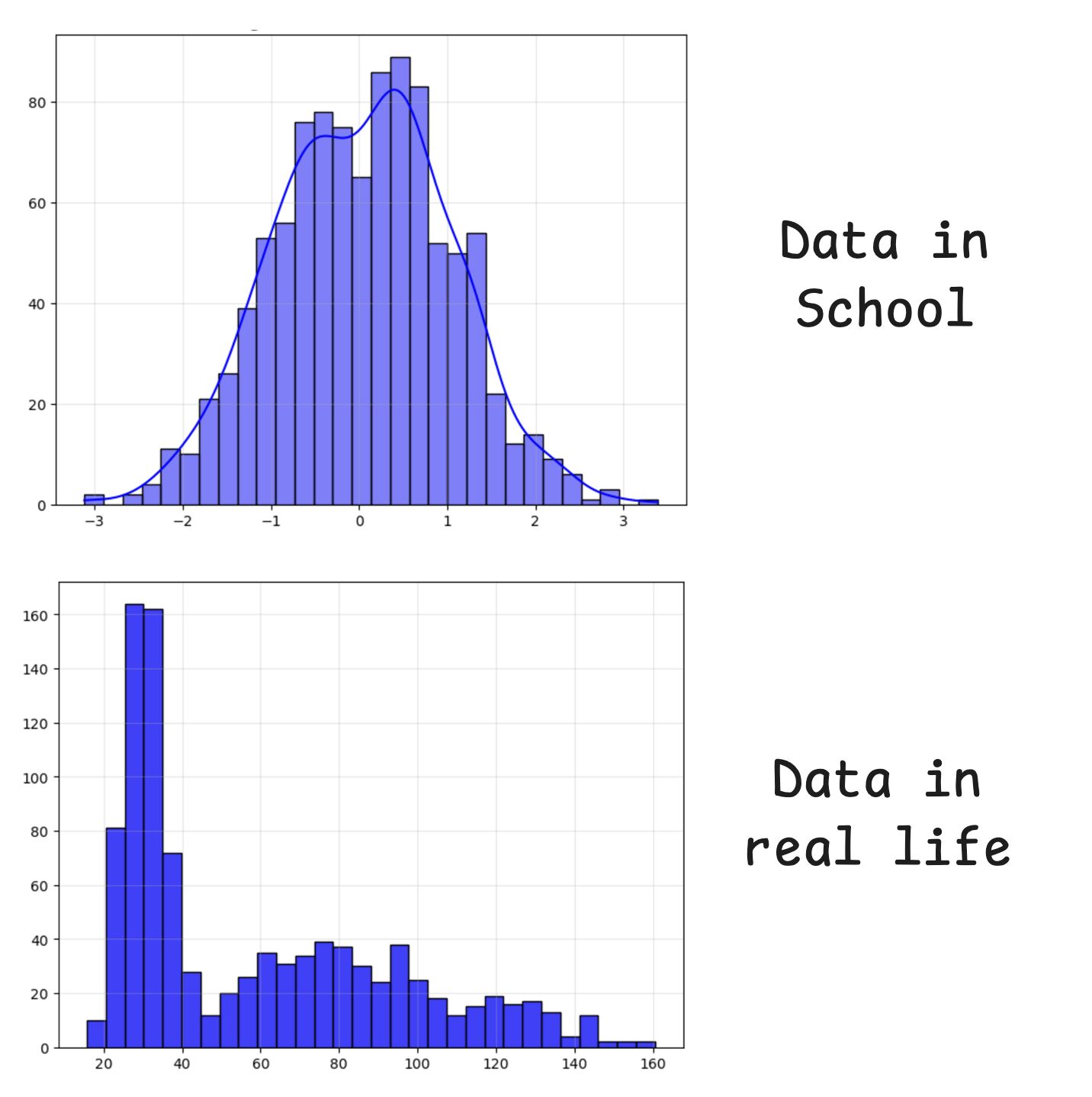
All Distributions are not “normal”

Real Life Data

Skewness

Skewness measures the asymmetry of a distribution around its mean.

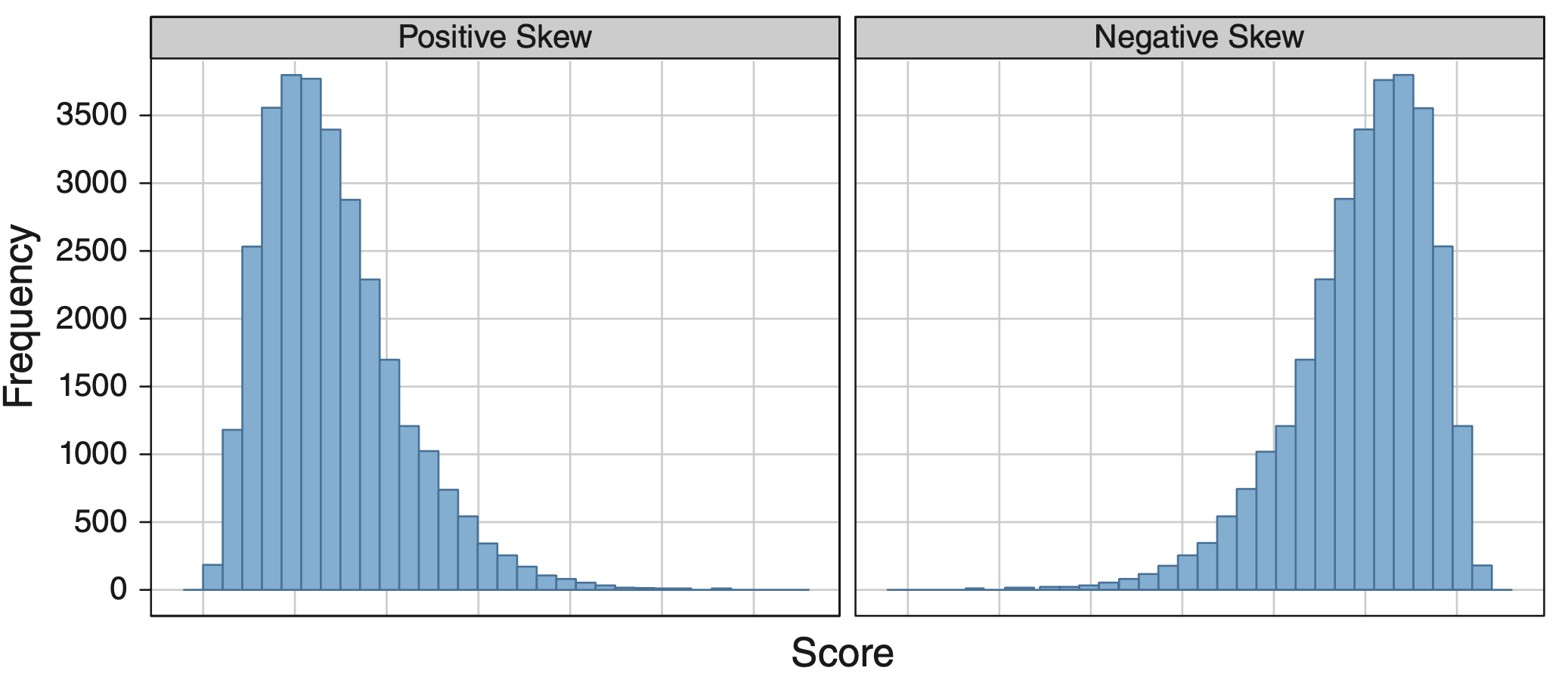
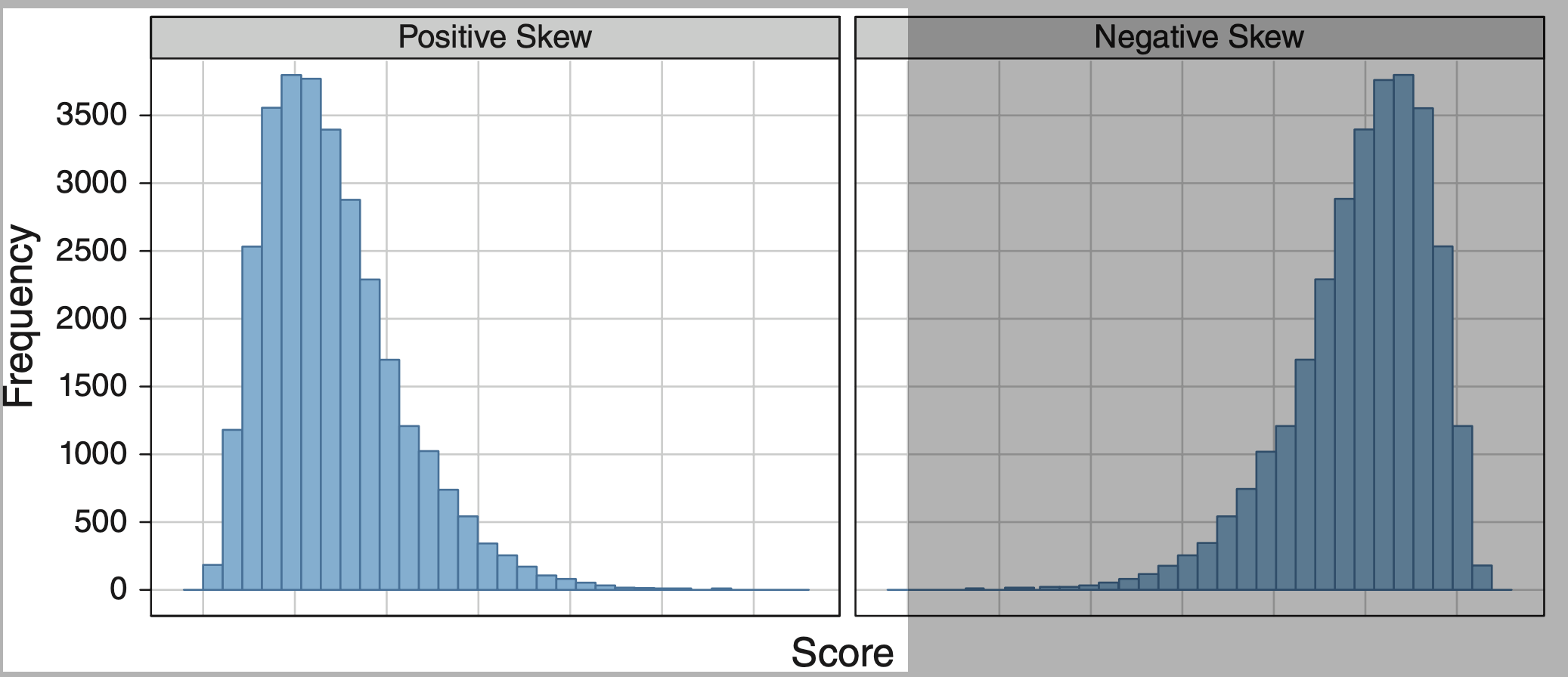
Positive Skew

“A longer tail on the right side.”

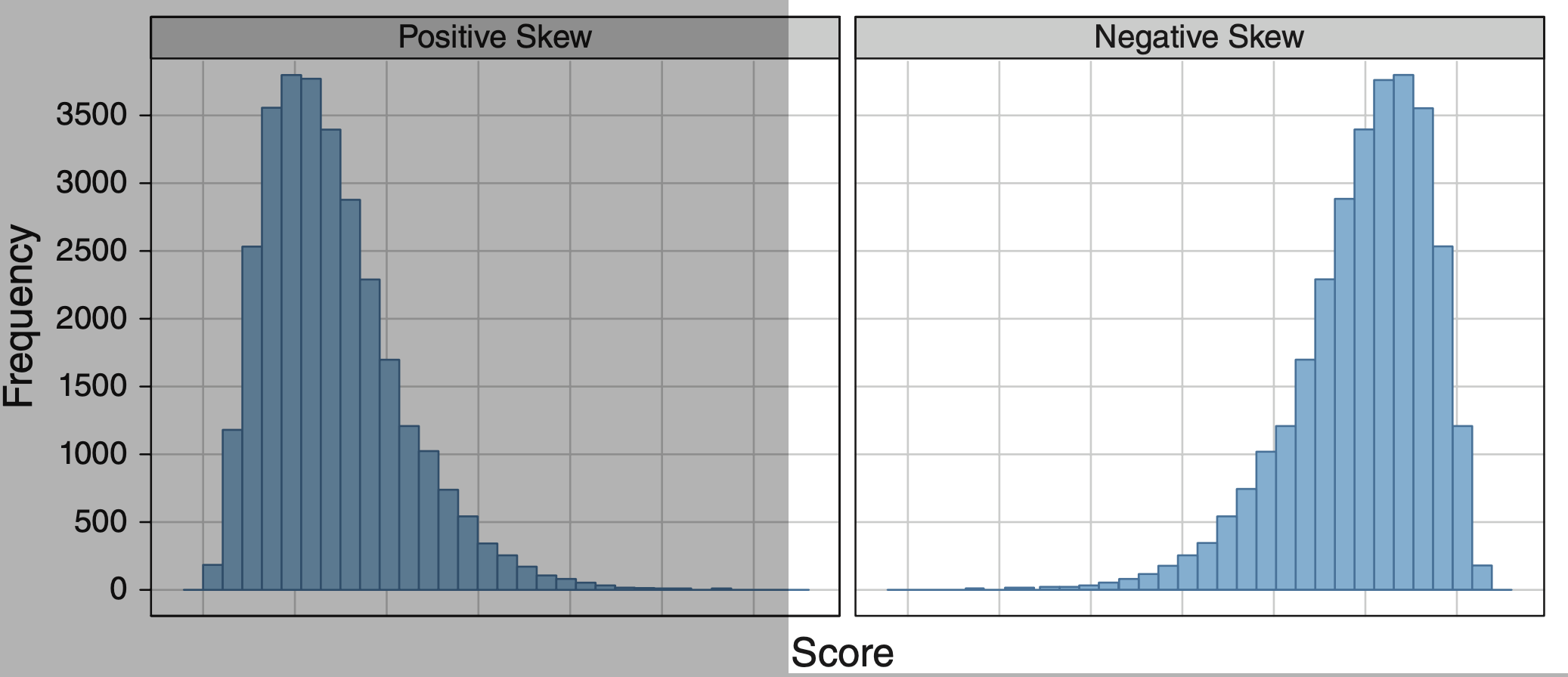
Negative Skew

A longer tail on the left side.

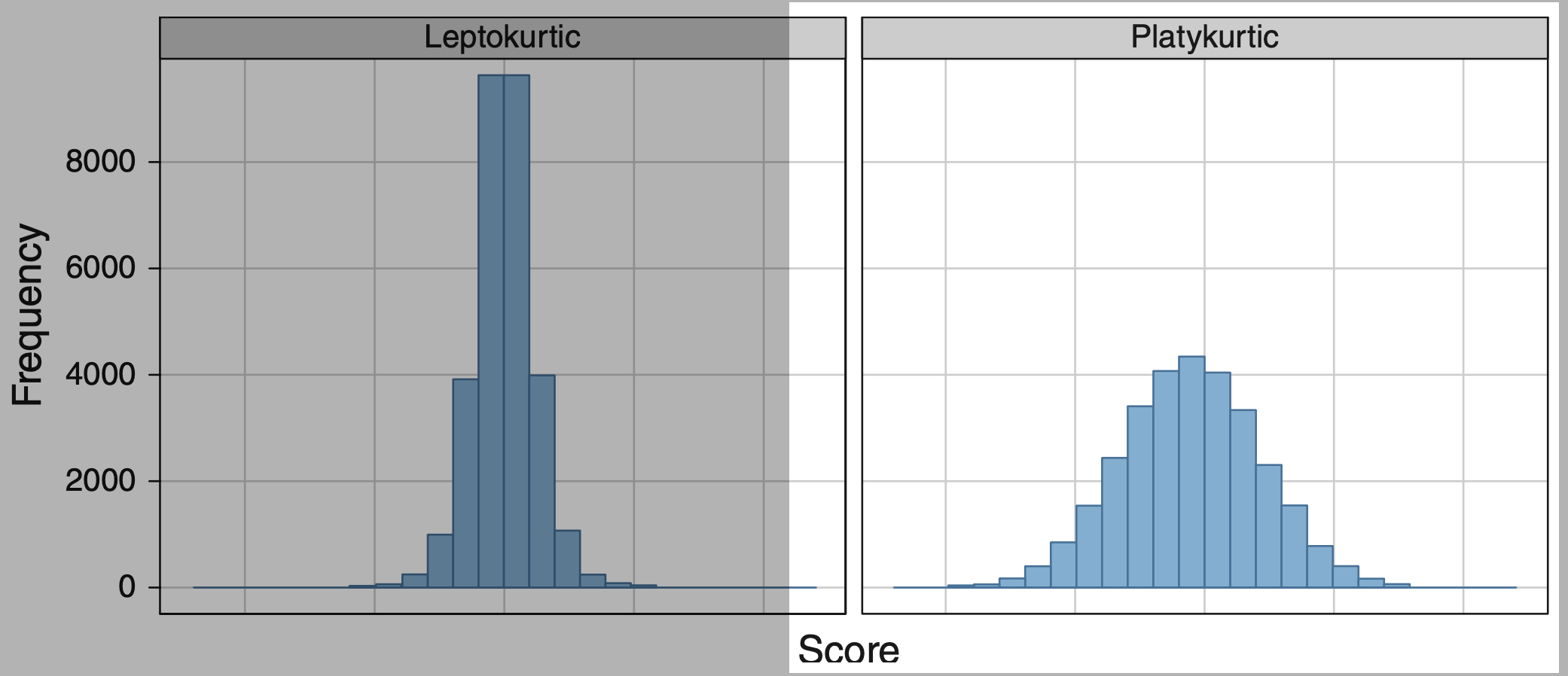
Kurtosis

Kurtosis measures the “tailedness” or sharpness of a distribution.

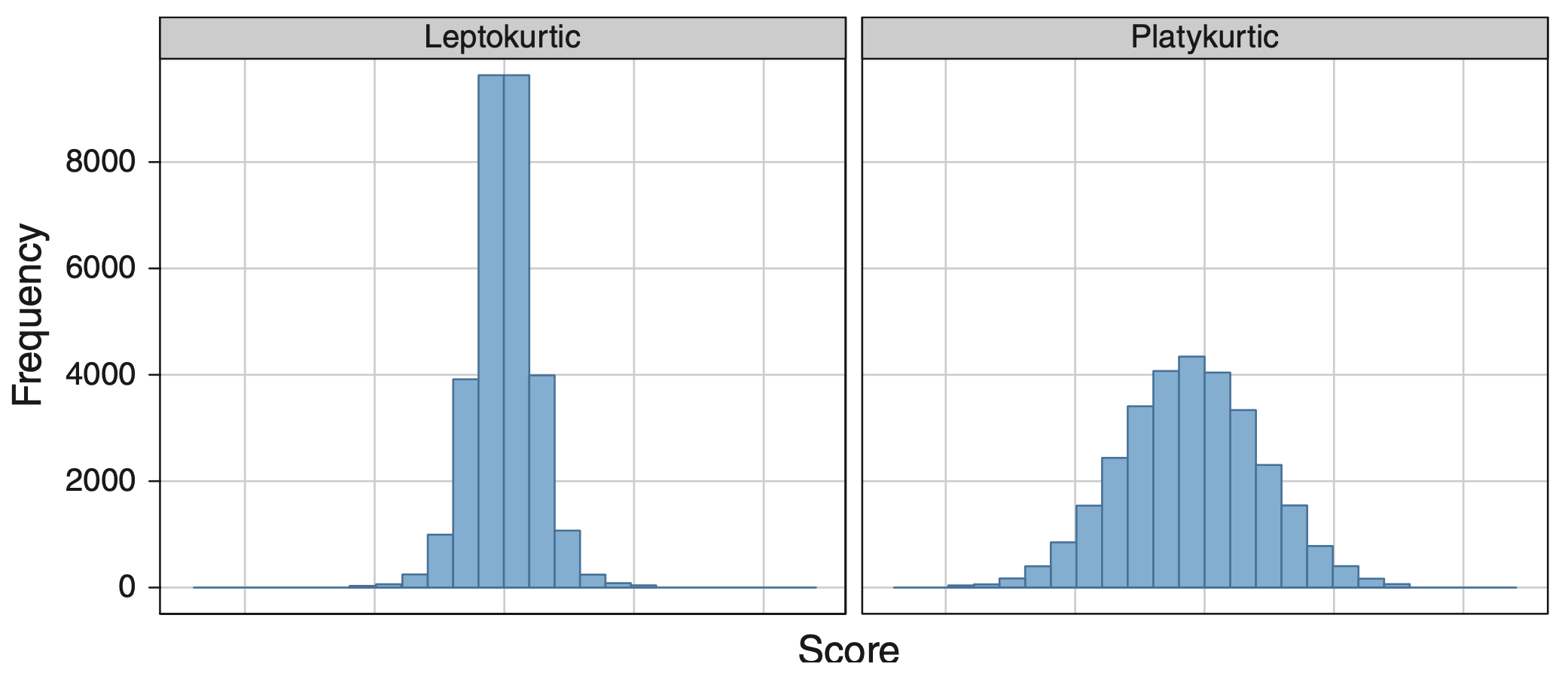
Leptokurtic

Heavy tails and sharp peak.

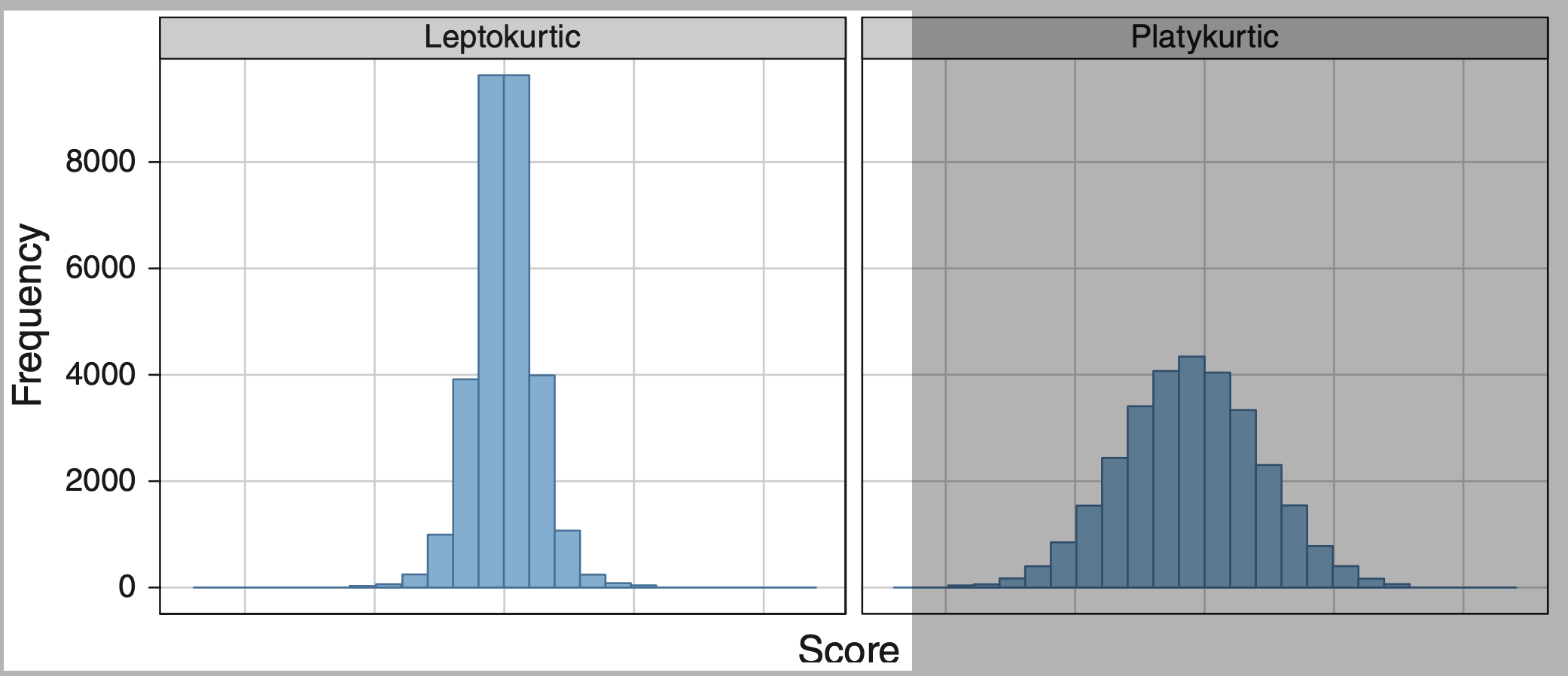
Platykurtic

Light tails and flatter peak.

Practice

Skewness

Symmetric Distribution: Skewness = 0.
Positive Skew: Tail on the right; Skewness > 0.
Negative Skew: Tail on the left; Skewness < 0.

Kurtosis

Mesokurtic: Normal distribution, Kurtosis ≈ 3.
Leptokurtic: Heavy tails, Kurtosis > 3.
Platykurtic: Light tails, Kurtosis < 3.

References